《Structural Dynamics and Vibration in Practice：An Engineering Handbook》

请叫我雷锋

《Structural Dynamics and Vibration in Practice：An Engineering Handbook》
结构动力学与实践振动：工程手册
作者：Douglas Thorby
出版社：BH
出版时间：2008年

《Structural Dynamics and Vibration in Practice：An Engineering Handbook》

《Structural Dynamics and Vibration in Practice：An Engineering Handbook》

《Structural Dynamics and Vibration in Practice：An Engineering Handbook》

《Structural Dynamics and Vibration in Practice：An Engineering Handbook》

目录
Preface xiii
Acknowledgements xv
Chapter 1 Basic Concepts 1
1.1 Statics, dynamics and structural dynamics 1
1.2 Coordinates, displacement, velocity and acceleration 1
1.3 Simple harmonic motion 2
1.3.1 Time history representation 3
1.3.2 Complex exponential representation 5
1.4 Mass, stiffness and damping 7
1.4.1 Mass and inertia 7
1.4.2 Stiffness 10
1.4.3 Stiffness and flexibility matrices 12
1.4.4 Damping 14
1.5 Energy methods in structural dynamics 16
1.5.1 Rayleigh’s energy method 17
1.5.2 The principle of virtual work 19
1.5.3 Lagrange’s equations 21
1.6 Linear and non-linear systems 23
1.7 Systems of units 23
1.7.1 Absolute and gravitational systems 24
1.7.2 Conversion between systems 26
1.7.3 The SI system 27
References 28
Chapter 2 The Linear Single Degree of Freedom System: Classical Methods 29
2.1 Setting up the differential equation of motion 29
2.1.1 Single degree of freedom system with force input 29
2.1.2 Single degree of freedom system with base motion input 33
2.2 Free response of single-DOF systems by direct solution of the equation
of motion 34
2.3 Forced response of the system by direct solution of the equation of motion 38
vii
Chapter 3 The Linear Single Degree of Freedom System: Response
in the Time Domain 45
3.1 Exact analytical methods 46
3.1.1 The Laplace transform method 46
3.1.2 The convolution or Duhamel integral 50
3.1.3 Listings of standard responses 53
3.2 ‘Semi-analytical’ methods 55
3.2.1 Impulse response method 56
3.2.2 Straight-line approximation to input function 56
3.2.3 Superposition of standard responses 56
3.3 Step-by-step numerical methods using approximate derivatives 59
3.3.1 Euler method 60
3.3.2 Modified Euler method 62
3.3.3 Central difference method 62
3.3.4 The Runge–Kutta method 65
3.3.5 Discussion of the simpler finite difference methods 69
3.4 Dynamic factors 70
3.4.1 Dynamic factor for a square step input 70
3.5 Response spectra 72
3.5.1 Response spectrum for a rectangular pulse 72
3.5.2 Response spectrum for a sloping step 74
References 76
Chapter 4 The Linear Single Degree of Freedom System: Response
in the Frequency Domain 77
4.1 Response of a single degree of freedom system with applied force 77
4.1.1 Response expressed as amplitude and phase 77
4.1.2 Complex response functions 81
4.1.3 Frequency response functions 83
4.2 Single-DOF system excited by base motion 86
4.2.1 Base excitation, relative response 87
4.2.2 Base excitation: absolute response 91
4.3 Force transmissibility 93
4.4 Excitation by a rotating unbalance 94
4.4.1 Displacement response 95
4.4.2 Force transmitted to supports 96
References 97
Chapter 5 Damping 99
5.1 Viscous and hysteretic damping models 99
5.2 Damping as an energy loss 103
5.2.1 Energy loss per cycle – viscous model 103
5.2.2 Energy loss per cycle – hysteretic model 104
5.2.3 Graphical representation of energy loss 105
5.2.4 Specific damping capacity 106
5.3 Tests on damping materials 108
viii Contents
5.4 Quantifying linear damping 108
5.4.1 Quality factor, Q 108
5.4.2 Logarithmic decrement 109
5.4.3 Number of cycles to half amplitude 110
5.4.4 Summary table for linear damping 111
5.5 Heat dissipated by damping 112
5.6 Non-linear damping 112
5.6.1 Coulomb damping 113
5.6.2 Square law damping 113
5.7 Equivalent linear dampers 114
5.7.1 Viscous equivalent for coulomb damping 115
5.7.2 Viscous equivalent for square law damping 116
5.7.3 Limit cycle oscillations with square-law damping 117
5.8 Variation of damping and natural frequency in structures with
amplitude and time 117
Chapter 6 Introduction to Multi-degree-of-freedom Systems 119
6.1 Setting up the equations of motion for simple, undamped,
multi-DOF systems 119
6.1.1 Equations of motion from Newton’s second law
and d’Alembert’s principle 120
6.1.2 Equations of motion from the stiffness matrix 120
6.1.3 Equations of motion from Lagrange’s equations 121
6.2 Matrix methods for multi-DOF systems 122
6.2.1 Mass and stiffness matrices: global coordinates 122
6.2.2 Modal coordinates 126
6.2.3 Transformation from global to modal coordinates 127
6.3 Undamped normal modes 132
6.3.1 Introducing eigenvalues and eigenvectors 132
6.4 Damping in multi-DOF systems 142
6.4.1 The damping matrix 142
6.4.2 Damped and undamped modes 143
6.4.3 Damping inserted from measurements 144
6.4.4 Proportional damping 145
6.5 Response of multi-DOF systems by normal mode summation 147
6.6 Response of multi-DOF systems by direct integration 155
6.6.1 Fourth-order Runge–Kutta method for multi-DOF systems 156
Chapter 7 Eigenvalues and Eigenvectors 159
7.1 The eigenvalue problem in standard form 159
7.1.1 The modal matrix 161
7.2 Some basic methods for calculating real eigenvalues and eigenvectors 162
7.2.1 Eigenvalues from the roots of the characteristic equation
and eigenvectors by Gaussian elimination 162
7.2.2 Matrix iteration 165
7.2.3 Jacobi diagonalization 168
Contents ix
7.3 Choleski factorization 177
7.4 More advanced methods for extracting real eigenvalues and eigenvectors 178
7.5 Complex (damped) eigenvalues and eigenvectors 179
References 180
Chapter 8 Vibration of Structures 181
8.1 A historical view of structural dynamics methods 181
8.2 Continuous systems 182
8.2.1 Vibration of uniform beams in bending 182
8.2.2 The Rayleigh–Ritz method: classical and modern 189
8.3 Component mode methods 194
8.3.1 Component mode synthesis 195
8.3.2 The branch mode method 208
8.4 The finite element method 213
8.4.1 An overview 213
8.4.2 Equations of motion for individual elements 221
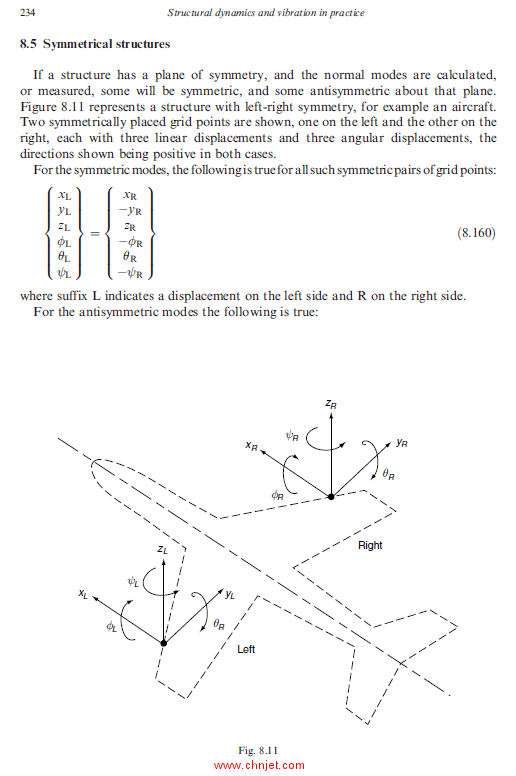
8.5 Symmetrical structures 234
References 235
Chapter 9 Fourier Transformation and Related Topics 237
9.1 The Fourier series and its developments 237
9.1.1 Fourier series 237
9.1.2 Fourier coefficients in magnitude and phase form 243
9.1.3 The Fourier series in complex notation 245
9.1.4 The Fourier integral and Fourier transforms 246
9.2 The discrete Fourier transform 247
9.2.1 Derivation of the discrete Fourier transform 248
9.2.2 Proprietary DFT codes 255
9.2.3 The fast Fourier transform 256
9.3 Aliasing 256
9.4 Response of systems to periodic vibration 260
9.4.1 Response of a single-DOF system to a periodic input force 261
References 265
Chapter 10 Random Vibration 267
10.1 Stationarity, ergodicity, expected and average values 267
10.2 Amplitude probability distribution and density functions 270
10.2.1 The Gaussian or normal distribution 274
10.3 The power spectrum 279
10.3.1 Power spectrum of a periodic waveform 279
10.3.2 The power spectrum of a random waveform 281
10.4 Response of a system to a single random input 286
10.4.1 The frequency response function 286
10.4.2 Response power spectrum in terms of the input
power spectrum 287
x Contents
10.4.3 Response of a single-DOF system to a broadband
random input 288
10.4.4 Response of a multi-DOF system to a single
broad-band random input 296
10.5 Correlation functions and cross-power spectral density functions 299
10.5.1 Statistical correlation 299
10.5.2 The autocorrelation function 300
10.5.3 The cross-correlation function 302
10.5.4 Relationships between correlation functions and power
spectral density functions 303
10.6 The response of structures to random inputs 305
10.6.1 The response of a structure to multiple random inputs 305
10.6.2 Measuring the dynamic properties of a structure 307
10.7 Computing power spectra and correlation functions using the discrete
Fourier transform 310
10.7.1 Computing spectral density functions 312
10.7.2 Computing correlation functions 314
10.7.3 Leakage and data windows 317
10.7.4 Accuracy of spectral estimates from random data 318
10.8 Fatigue due to random vibration 320
10.8.1 The Rayleigh distribution 321
10.8.2 The S–N diagram 322
References 324
Chapter 11 Vibration Reduction 325
11.1 Vibration isolation 326
11.1.1 Isolation from high environmental vibration 326
11.1.2 Reducing the transmission of vibration forces 332
11.2 The dynamic absorber 332
11.2.1 The centrifugal pendulum dynamic absorber 336
11.3 The damped vibration absorber 338
11.3.1 The springless vibration absorber 342
References 345
Chapter 12 Introduction to Self-Excited Systems 347
12.1 Friction-induced vibration 347
12.1.1 Small-amplitude behavior 347
12.1.2 Large-amplitude behavior 349
12.1.3 Friction-induced vibration in aircraft landing gear 350
12.2 Flutter 353
12.2.1 The bending-torsion flutter of a wing 354
12.2.2 Flutter equations 358
12.2.3 An aircraft flutter clearance program in practice 360
12.3 Landing gear shimmy 362
References 366
Contents xi
Chapter 13 Vibration testing 367
13.1 Modal testing 368
13.1.1 Theoretical basis 368
13.1.2 Modal testing applied to an aircraft 369
13.2 Environmental vibration testing 373
13.2.1 Vibration inputs 373
13.2.2 Functional tests and endurance tests 374
13.2.3 Test control strategies 375
13.3 Vibration fatigue testing in real time 376
13.4 Vibration testing equipment 377
13.4.1 Accelerometers 377
13.4.2 Force transducers 378
13.4.3 Exciters 378
References 385
Appendix A A Short Table of Laplace Transforms 387
Appendix B Calculation of Flexibility Influence Coefficients 389
Appendix C Acoustic Spectra 393
Index 397


专业书籍
下载地址：（回复后可见）

游客，如果您要查看本帖隐藏内容请回复

璀璨星空

谢谢分享。
来自: 微社区

jjj

Good book, thanks

oygx210

thanks

御锋

谢谢

GOOWOO

好书

慢慢来123321

谢谢

donglake

谢谢雷锋。。。。。。。。。。。。。。

xuewuhen999

谢谢

confuze

学习雷锋